部分整体相同的数学问题研究

• 连分数
• 无限式
• 无限电阻
• 马尔科夫链无穷递推

分形学中, 部分 = 整体是一个很明显的特征, 不过对于高中生而言, 这个概念并不常用.

但是部分 = 整体的思想却比较有用, 这里分享一下高中时期发现的一些谈不上技巧, 只能算是小感悟的东西吧.

---

连分数

咱第一次接触连分数都概念是妈咪叔讲解的BV1ZJ411c7PS, 这里分享一下如何使用无限连分数表示自然数开根.

对于自然数 $n$ , 设 $x^2=n$ , 则有:

$$\begin{gathered} x^2-1=n-1 \\ (x+1)(x-1)=n-1 \end{gathered}$$

由于是根式, 则 $n>0$ , 必然 $x>0,x+1>0$

$$\begin{gathered} x-1=\frac{n-1}{1+x} \\ x=1+\frac{n-1}{1+x} \end{gathered}$$

此时, 等式左右均存在 $x$ , 我们将左边的 $x$ 代入右侧, 也就是将 $x=1+\frac{n-1}{1+x}$ 代入右侧分母 $x$ 的位置.

这里可以比较乱, 就把左右先看做不一样的字母即可.

$$x=1+\frac{n-1}{2+\frac{n-1}{1+x}}$$

同理, 接着将 $x=1+\frac{n-1}{1+x}$ 代入右侧:

$$x=1+\frac{n-1}{2+\frac{n-1}{2+\frac{n-1}{2+\frac{n-1}{\ddots }}}}$$

将 $x$ 替换为 $\sqrt{n}$ , 则:

$$\sqrt{n}=1+\frac{n-1}{2+\frac{n-1}{2+\frac{n-1}{2+\frac{n-1}{\ddots }}}}$$

这样我们就把一个自然数的平方根用循环结构表示了出来, 我们可以取一定数目的循环量, 用于估算某数的平方根.

例如:

$$\begin{array}{c}\begin{array}{rl}\sqrt{2}& =1+\frac{1}{2+\frac{1}{2+\frac{1}{2+\frac{1}{\ddots }}}}\\ & \approx 1+\frac{1}{2+\frac{1}{2+\frac{1}{2+\frac{1}{1}}}}\\ & =1+\frac{7}{17}\\ & =1.4117\end{array}\end{array}$$

和一般记忆的值1.414精度还是有一定差距的, 但我们仅取了3个循环节, 几乎毫无计算量, 这个数据还是可以的.

无限式

尝试计算

$$1+2\times (1+2\times (1+2\times (1+2\times (\cdots ))))$$

当我们尽量取大量的循环结构时, 结果会越来越靠近一个值.

而且当取值足够多时, 再增加循环节, 对结果影响越来越小, 所以我们可以一直计算直到达到浮点数 精度上限.

我们令该式等于 $x$ , 观察发现:

$$x=1+2\times (\underset{\text{x}}{\underline{1+2\times (1+2\times (1+2\times (\cdots )))}})$$

即

$$\begin{gathered} x=1+2\times x \\ x=-1 \end{gathered}$$

该式子也是部分 = 整体的思想, 直接进行替换, 快速求出整体的值.

同理, 多截取一部分少截取一部分, 结果是一样的.

$$\begin{array}{c}\begin{array}{rl}x& =1+2x\\ & =1+2\times (1+2x)\\ & =1+2\times (1+2\times (1+2x))\end{array}\end{array}$$

上述 $x$ 取值都相同.

无限电阻

无限长梯形电阻网络

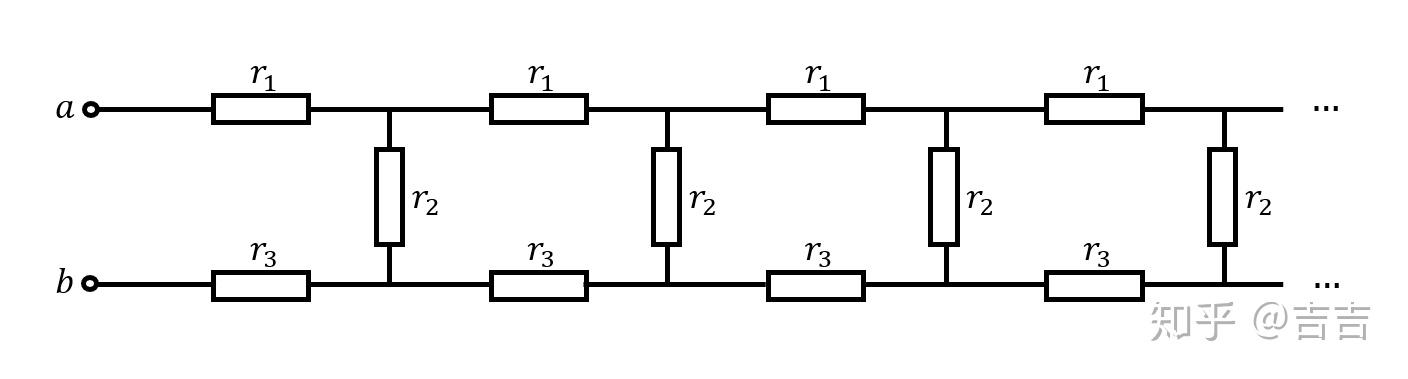
如图所示, 每个小电阻阻值为1Ω, 求总a, b之间的总电阻.

问题来自知乎

该电阻网络也可以认为部分 = 整体, 因为当我们将最左侧三个电阻独立出来时, 右侧所以电阻可以看做并联在 $r_2$ 两端的a, b总电阻, 即:

$$\begin{gathered} R=r_1+r_2//R+r_3 \\ R=1+\frac{R}{1+R}+1 \end{gathered}$$

解得 $R=1+\sqrt{3}$ .

马尔科夫链无穷递推

这里先讲一道题, 关于马尔科夫链其他知识稍后再分享.

武汉二调T14

“布朗运动”是指微小颗粒永不停息的无规则随机运动，在如图所示的试验容器中，容器由三个仓组成，某粒子作布朗运动时每次会从所在仓的通道口中随机选择一个到达相邻仓或者容器外，一旦粒子到达容器外就会被外部捕获装置所捕获，此时试验结束. 已知该粒子初始位置在1号仓，求试验结束时该粒子是从1号仓到达容器外的概率.

布朗运动

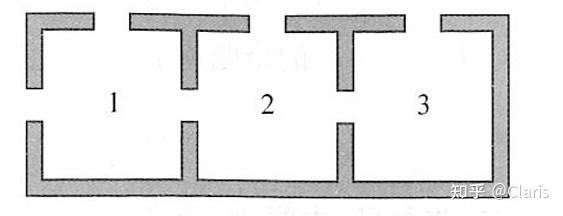
问题来自知乎

我们尝试从传统条件概率的思想分析这道题:

• 粒子之间从1离开, 概率为 $\frac{2}{3}$
• 粒子来到2, 从2离开, 概率为 $\frac{1}{3}\times \frac{1}{3}$
• 粒子来到2, 再回到1, 概率为 $\frac{1}{3}\times \frac{1}{3}$ , 之后将重复整个过程: 直接离开, 来到2离开, 来带2回来, ...
• 粒子来到2, 再来到3, 从3离开, 概率为 $\frac{1}{3}\times \frac{1}{3}\times \frac{1}{2}$
• 粒子来到2, 再来到3, 然后回到2, 概率为 $\frac{1}{3}\times \frac{1}{3}\times \frac{1}{2}$ , 但之后又要重复到2的过程: ...

上述分析中, 我们发现, 从2回到1, 和最开始直接从1出发没有区别, 满足部分 = 整体的思想. 此外, 从2到3再回2, 与直接到2也没有区别, ...

假设从1离开的概率为x, 则有:

$$x=\underset{\text{直接离开}}{\frac{2}{3}}+\underset{\text{到2}}{\frac{1}{3}}(\underset{\text{回1}}{\frac{1}{3}}x+\underset{\text{到3回2}}{\frac{1}{3}\times \frac{1}{2}}(\underset{\text{回1}}{\frac{1}{3}}x+\underset{\text{到3回2}}{\frac{1}{3}\times \frac{1}{2}}(\underset{\text{回1}}{\frac{1}{3}}x+\underset{\text{到3回2}}{\frac{1}{3}\times \frac{1}{2}}(\cdots ))))$$

再次发现循环结构, 我们再简化一下, 记粒子在1且最终从1离开的概率为a, 粒子在2但最终从1离开的概率为b, 则存在:

$$\begin{gathered} a=\underset{\text{直接离开}}{\frac{2}{3}}+\underset{\text{到2}}{\frac{1}{3}}b \\ b=\underset{\text{回1}}{\frac{1}{3}}a+\underset{\text{到3回2}}{\frac{1}{3}\times \frac{1}{2}}b \end{gathered}$$

最终解方程即可:

$$\{\begin{array}{l}a=\frac{10}{13}\\ b=\frac{4}{13}\end{array}$$

即从1离开概率为 $\frac{10}{13}$